第二章 描述性统计

均值（mean）和平均值(average)

均值的计算：µ = 1/n *∑x

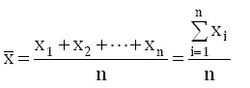
均值和平均值的区别：

样本的“均值”是根据上述公式计算出的一个汇总统计量

“平均值”是若干种可以用于描述样本的典型值或集中趋势的汇总统计量之一

例如：3个1磅的南瓜，2个3磅的南瓜和1个579磅的南瓜，其平均值没有意义，即“典型”的南瓜不存在。

方差（variance）

用于描述数据的分散的情况。

计算公式：

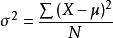
其中µ为均值

标准差：方差的平方根。

分布

描述了各个值出现的频繁程度

表示分布最常用的方法：直方图(histogram)，用于展示各个值出现的频数和概率。

直方图可以直观的展现出数据的以下特征：

• 众数（mode）：分布中出现次数最多的值
• 形状：对称性
• 异常值：远离众数的值

但通常比较两个直方图的意义不大，因为很有可能其差异是由于样本数量的不同产生的。

频数（frequency）：数据集中一个值出现的次数。

概率(probability)：频数除以样本数量n。

归一化（normalization）:把频数转换为概率。

概率质量函数 （Probability Mass Function PMF）：值到概率的映射，归一化后的直方图。

给定一个PMF，也可以计算均值和方差。

放大差异

可以将两个直方图进行相减并乘以100。

相对风险

代表两个概率的比值。

例如：A发生的概率是18.2%，B发生的概率为16.8%，因此相对概率为1.08，意味着A比B更有可能发生的概率是8%。